Research
Covariance Dynamics in Data Assimilation
The time evolution of the estimation error covariance is an important aspect of modern data assimilation algorithms and numerical weather prediction. While the evolution of the state of the atmosphere is generally well-understood, there are still aspects of how the covariance evolves in time that we don’t fully understand. In part of my research, I study covariance propagation, namely the equations that describe the time evolution of the covariance and how solutions to these equations are approximated in practice. By carefully examining both the underlying partial differential equations and numerical schemes used to approximate solutions, my work uncovers a fundamental problem that helps to explain a long misunderstood phenomena observed in chemical tracer data assimilation.
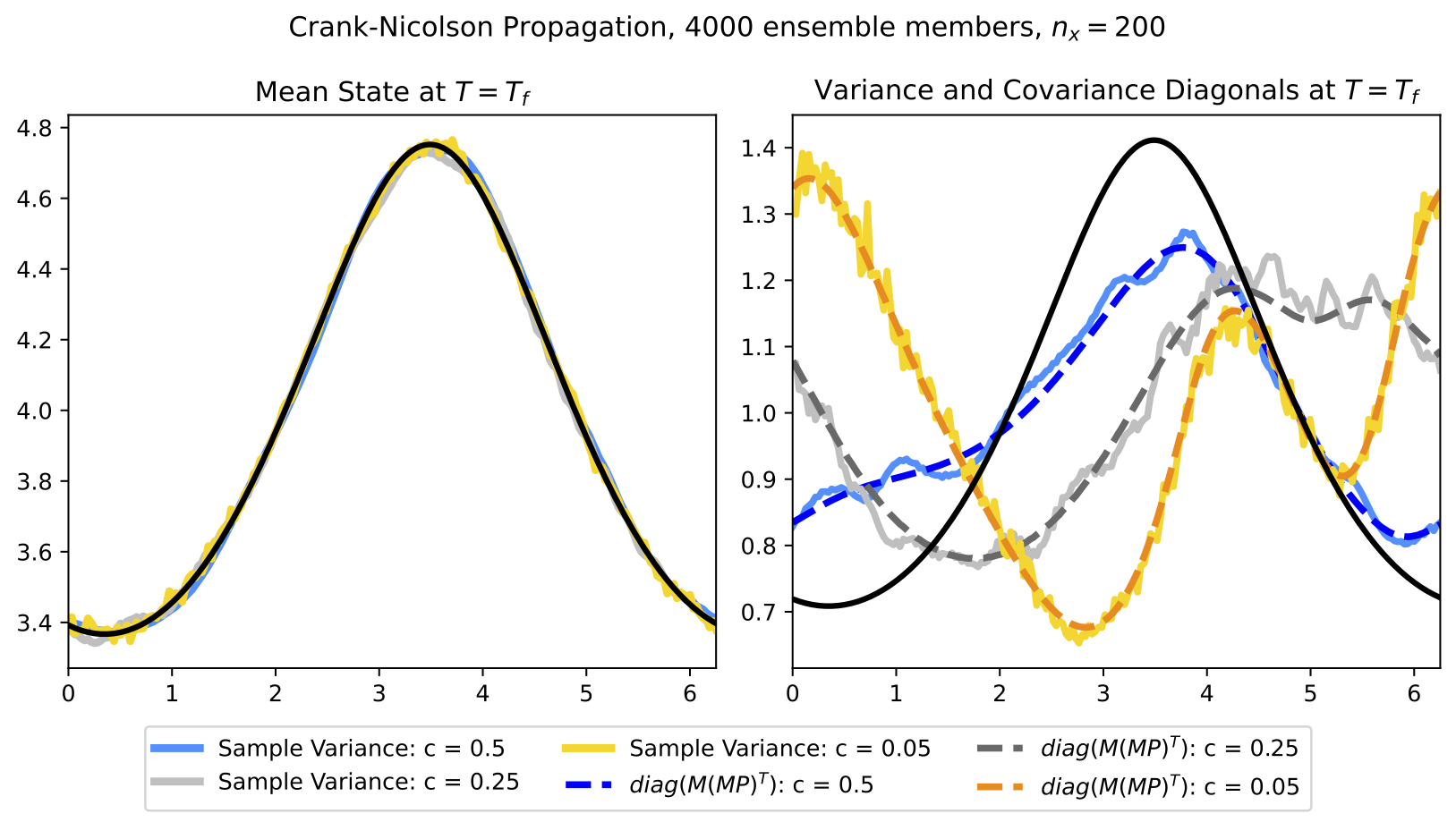 The above figure is an example of how variances propagated by using standard, full-rank covariance propagation, as in a Kalman filter (dashed color), and Monte Carlo approximations of the variance estimated by propagating an ensemble of states, as in an ensemble Kalman filter (solid color), are severely inaccurate compared to the exact variance (solid black). We observe not only variance loss, but also variance gain, both of which can cause problems during data assimilation. This is in contrast with the approximation of the mean state from the same propagated ensemble (left panel), which is fairly accurate. The underlying cause of this inaccuracy is a discrepancy between the structure of these discrete propagation schemes and the continuum covariance dynamics described by partial differential equations.
The above figure is an example of how variances propagated by using standard, full-rank covariance propagation, as in a Kalman filter (dashed color), and Monte Carlo approximations of the variance estimated by propagating an ensemble of states, as in an ensemble Kalman filter (solid color), are severely inaccurate compared to the exact variance (solid black). We observe not only variance loss, but also variance gain, both of which can cause problems during data assimilation. This is in contrast with the approximation of the mean state from the same propagated ensemble (left panel), which is fairly accurate. The underlying cause of this inaccuracy is a discrepancy between the structure of these discrete propagation schemes and the continuum covariance dynamics described by partial differential equations.
Relevant Publications
Gilpin, S., 2025: Inaccuracy of ensemble-based covariance propagation, beyond sampling error, https://doi.org/10.48550/arXiv.2508.16567.
Gilpin, S., Matsuo, T., and Cohn, S.E., 2025: Inaccuracy of the variance evolution associated with discrete covarince propagation, Q. J. Roy. Meteor. Soc., 1-26, https://doi.org/10.1002/qj.5016.
Gilpin, S., Matsuo, T., and Cohn, S.E., 2022: Continuum covariance propagation for understanding variance loss in advective systems, SIAM/ASA J. Uncertainty Quantification, 10, 886 – 914, https://doi.org/10.1137/21M1442449.
Covariance Modeling and Estimation
Covariance modeling is a challenging and highly relevant problem in both spatial statistics and data assimilation applications. Often, parametric correlation functions are used to construct correlation fields from a finite number of parameters to then model covariances. The figure below is an example of the Generalized Gaspari-Cohn correlation function from Gilpin et al., (2023), which generalizes the Gaspari-Cohn correlation function commonly used in data assimilation applications. The Generalized Gaspari-Cohn correlation function can generate correlations that are highly anisotropic and compactly supported on non-uniform domains, making it a powerful tool for covariance modeling.
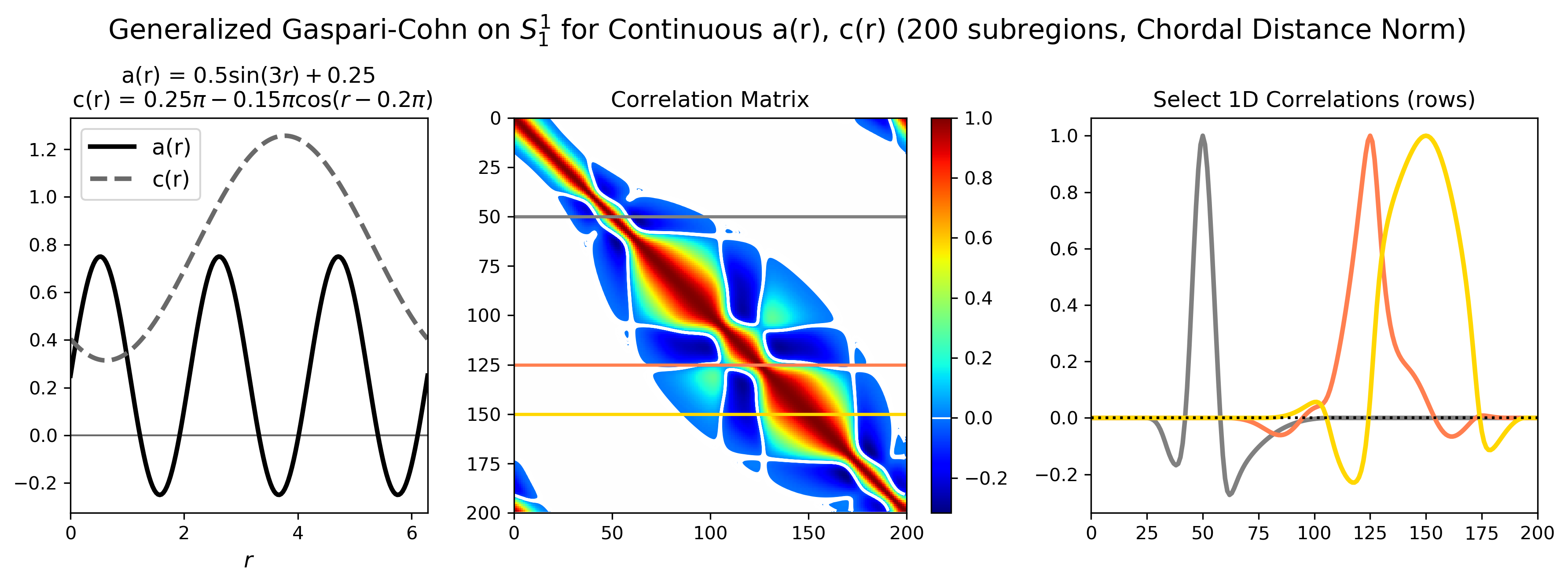
The Generalized Gaspari-Cohn (GenGC) correlation function opens the door to building new covariance localization techniques for data assimilation applications. Covariance localization, which tapers sample correlations as a function of distance, is applied in high-dimensional, low sample size problems to improve covariance estimates. In ensemble-based data assimilation schemes, the most frequently used localization function is GenGC’s predecessor, the Gaspari-Cohn correlation function, which depends on a single cut-off parameter that can depend on space, time, observation type, and requires tuning. GenGC provides a flexible alternative, where new localization functions can be build that maintain their compact support while incorporating more structural information to capture inhomogeneous and anisotropic features that Gaspari-Cohn cannot. Gilpin et al., (2025b) is the first to implement GenGC for covariance localization in an ensemble Kalman filter, where its performance is competitive with standard localization techniques using Gaspari-Cohn.
Relevant Publications
Gilpin, S., Morzfeld, M., and Lin, K. K.: 2025: Numerical study of high-dimensional covariance estimation and localization for data assimilation. https://doi.org/10.48550/arXiv.2508.18299.
Gilpin, S., Matsuo, T., and Cohn, S.E., 2023: A generalized, compactly-supported correlation function for data assimilation applications, Q. J. Roy. Meteor. Soc., 149, 1953 - 1989, https://doi.org/10.1002/qj.4490.
Gilpin, S., 2023: A generalized Gaspari-Cohn correlation function, (v1.0), Zenodo, https://doi.org/10.5281/zenodo.7859258.
Radio Occultation
Radio occultation (RO) is a method of remote sensing used to observe Earth’s atmosphere. As radiowaves emitted from GPS satellites traverse quasi-horiztontally through our atmosphere, they bend (refract) depending on the atmospheric state. Low-Earth orbiting (LEO) satellites then receive these radiowave signals, which can ultimately produce vertical profiles of lower atmospheric and ionospheric quantities. RO observations are assimilated into numerical weather prediction models and have been shown to make a significant impact.
While working for the Constellation Observing System for Meteorology, Ionosphere and Climate (COSMIC) Program at UCAR, I worked on projects with the aim of improving co-locations methods for RO-radiosonde comparisons and investigating the errors introduced during vertical interpolation of refractivity during RO data assimilation.
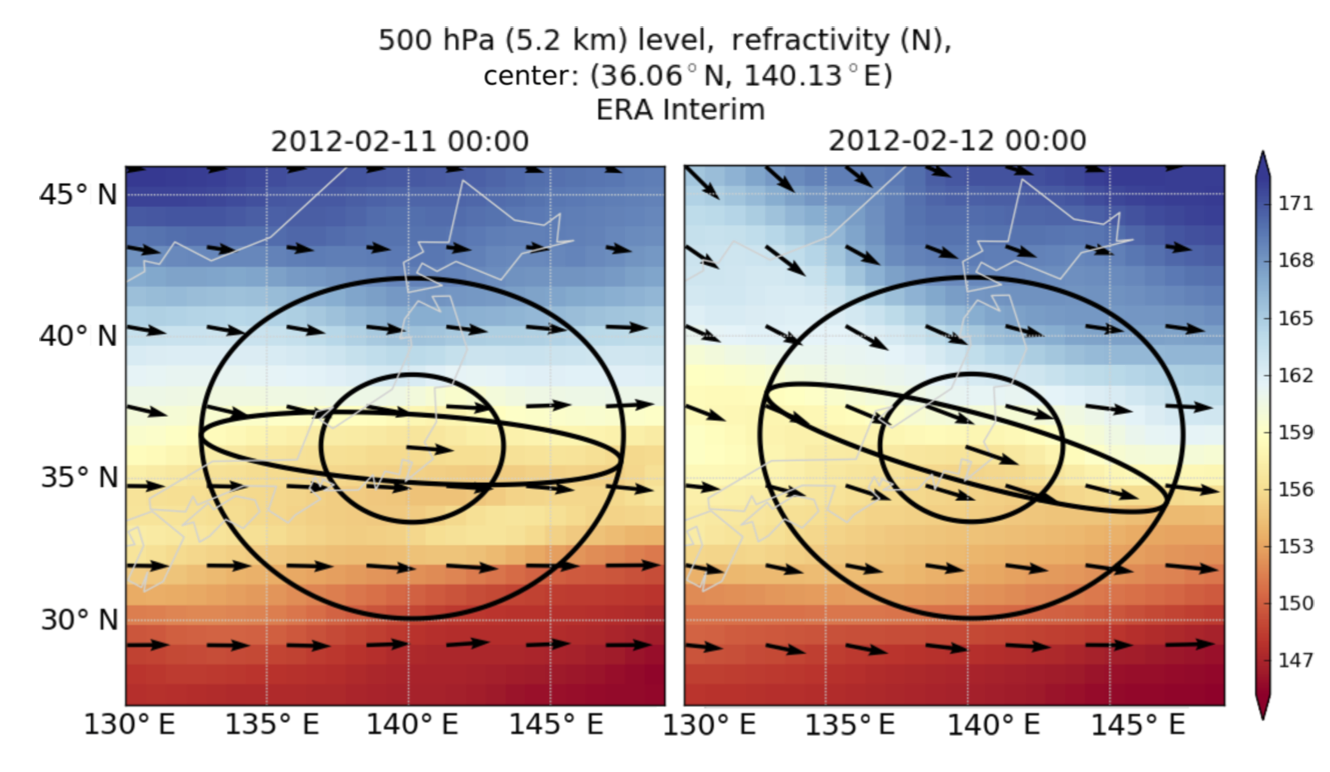 Traditional co-location methods used for comparing atmospheric observations are circles: observations are compared within a fixed distance of a specified location. In Gilpin et. al., (2018), we propose to co-locate observations using ellipses oriented along the direction of the wind, rather than circles, to reduce representativeness errors during RO-radiosonde comparisons.
Traditional co-location methods used for comparing atmospheric observations are circles: observations are compared within a fixed distance of a specified location. In Gilpin et. al., (2018), we propose to co-locate observations using ellipses oriented along the direction of the wind, rather than circles, to reduce representativeness errors during RO-radiosonde comparisons.
Relevant Publications
Gilpin, S., Rieckh, T., and Anthes, R., 2018: Reducing representativeness errors during radio occultation – radiosonde comparisons, Atmos. Meas. Tech., 11, 269-289, https://doi.org/10.5194/amt-11-1-2018.
Gilpin, S., Anthes, R., and Sokolovskiy, S., 2019: Sensitivity of forward-modeled bending angles to vertical interpolation of refractivity for radio occultation data assimilation, Mon. Wea. Rev., 147, 2567–2582, https://doi.org/10.1175/MWR-D-18-0223.1
